Instrucciones
Usted tiene las siguientes opciones en este simulador para moléculas pequeñas tanto inorgánicas como orgánicas.
- En la parte superior, aparecen los botones 2D y 3D para que pueda observar el modelo en dos o tres dimensiones.
- A continuación se presenta el modelo en dos o tres dimensiones.
- "Search" puede ser utilizado para buscar alguna molécula, escribiendo el nombre en inglés, por ejemplo al escribir, sulphuric acid (ácido sulfúrico).
- Color de fondo, sirve seleccionar el color del fondo del modelo en tres dimensiones.
- Acercar +, acerca el modelo.
- Acercar -, aleja el modelo.
- Girar X, Y, Z, para girar el modelo en tres dimensiones en los ejes x, y, z.
- Alambres, varillas y pelotas y varillas, para cambiar el modelo en tres dimensiones en esas representaciones.
- Energía, aparce en la parte superior la energía de la molécula en kJ/mol o kcal/mol.
- Minmizar por MMFF94, normalmente las estructuras iniciales que se crean en los simuladores poseen energías mucho mayores a las que tendría un objeto real, por esta razón, se utilizan algoritmos para calcular las posiciones y fuerzas originales, con el objetivo de minimizarlas y que sean más realistas.
- Arrastrar Minimizar, usted puede arrastrar un átomo, soltarlo y entonces el sistema hace un cálculo de minimización de energía.
- Simetría, muestra los planos de simetría en la molécula.
- Editar, puede editar la molécula agragando o quitando átomos y enlaces.
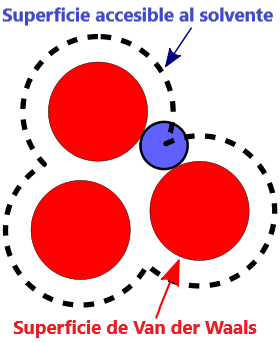
- Superficie VDW, la superficie de van der Waals de una molécula es una representación abstracta o modelo de esa molécula, que ilustra dónde, en términos muy generales, podría haber una superficie para la molécula en función de los cortes duros de los radios de van der Waals para átomos individuales, y representa una superficie a través de la cual la molécula podría concebirse interactuando con otras moléculas.
- PEM es el mapa de potencial electrostático.
- Carga parcial calcula la carga parcial de cada átomo.
- Tetraedros, para el caso que exista alguna átomo tetraédrico.
- Dipolos enlaces, para ver el los dipolos de todos los enlaces.
- Dipolo molecular, para ver el momento dipolar resultante de toda la molécula.
- Hibridación sp, sp2 y sp3, para ver la hibridacion del átomo de carbono.
- Anillo aromático, muestra los anillos aromáticos.
- Heteroátomo, muestra los heteroátomos en heterociclos.
- C quiral (nomenclatura R/S) y E/Z para isomería geométrica en alquenos, los descriptores R/S permiten indicar en un compuesto orgánico la configuración (la disposición espacial de los sustituyentes) de un carbono o centro quiral, estereocentro o centro estereogénico, que es el caso de un átomo de carbono con cuatro sustituyentes diferentes. Se añade R o S entre paréntesis como prefijo delante del nombre de la molécula orgánica. En caso de ser más de uno el centro estereogénico, separados por coma se indica el descriptor R o S de cada uno, precedido del número o localizador que identifica su posición.
- Invertir R/S, para cambiar la quiralidad.
- Nomenclatura E/Z en Alquenos, el sistema tradicional para nombrar los isómeros geométricos de un alqueno, en el que los mismos grupos están dispuestos de manera diferente, es nombrarlos como cis o trans. Sin embargo, es fácil encontrar ejemplos donde el sistema cis-trans no se aplica fácilmente.
- N electrones, O electrones y S electrones, para ver los electrones libres del nitrógeno, oxígeno y azufre.
- C primario, C secundario, C terciario, C cuaternario, identifica la clasificación de los átomos de carbono.
- Dadores y aceptores de puentes de hidrógeno, señala los átomos que pueden dar o aceptar puentes de hidrógeno
- Botón 2D, cuando escoge el botón 2D, la aplicación tiene su propio menú y quedan inhabilitados todos los botones 3D.
Soluciones

Escuchar Podcast
Haz clic en el botón para cargar y reproducir el audio.
Video Explicativo
Presentación Resumida
Para mejor experiencia en celular, abre la guía directamente:
Abrir Guía PDFLa presentación contiene gráficas de alta calidad.
Herramientas para el Trabajo: ¿Masa o Volumen?
Imagina que estás en un laboratorio de alta precisión. Tienes un sólido que debes medir con exactitud milimétrica. ¿Qué usas? La Masa. Ahora, imagina que estás en una fábrica de bebidas embotellando miles de litros por hora. ¿Pesarías cada botella? No, usarías el Volumen por su velocidad.
Concepto Clave
No existe una "mejor" unidad de concentración. Existen diferentes herramientas para diferentes trabajos:
- Porcentaje en Masa (% m/m): La herramienta de la precisión. (Química Analítica, Sólidos).
- Porcentaje en Volumen (% v/v): La herramienta de la eficiencia. (Industria, Líquidos).
- Porcentaje Masa-Volumen (% m/v): El híbrido práctico. (Medicina, Farmacia).
1. Porcentaje en Masa (% m/m): La Precisión
Usado cuando la temperatura varía (el volumen cambia con el calor, la masa no) o cuando se requiere máxima exactitud.
La Fórmula
| % m/m = | Masa de Soluto (g) | x 100 |
| Masa de Solución (g) |
Recuerda: Masa Solución = Masa Soluto + Masa Solvente
Ejemplo N° 1 (Básico)
Se prepara una solución mezclando 1.00 g de etanol con 100.0 g de agua. Calcule el % en masa.
1. Datos: Soluto = 1.00 g | Solvente = 100.0 g
2. Cálculo de Solución Total: 1.00 g + 100.0 g = 101.0 g solución
3. Factor Unitario:
| 1.00 g Soluto | x 100 = | 0.99% m/m |
| 101.0 g Solución |
Ejemplo N° 2 (Aplicación Médica)
En un hospital se requiere preparar 500 g de suero glucosado al 5.0% m/m. ¿Cuántos gramos de glucosa se deben pesar?
1. Análisis:
- Masa total deseada = 500 g
- Concentración = 5.0% (5.0 g glucosa / 100 g suero)
2. Cálculo directo masa-masa:
| 500 g Suero | x | 5.0 g Glucosa | = | 25.0 g Glucosa |
| 1 | 100 g Suero |
Desafío Guiado: Resolviendo como un Experto
Ejemplo N° 3
Calcule la masa de agua (g) que debe agregarse a 10.0 g de NaNO3 para preparar una solución al 2.00% m/m.
Identificar Datos y Objetivo
- Tenemos (Soluto): 10.0 g de NaNO3
- Queremos (Concentración): 2.00% m/m (Significa: 2.00 g soluto por cada 100 g solución)
- Objetivo: Encontrar los gramos de agua (Solvente).
Estrategia con Factor Unitario
En lugar de memorizar fórmulas, usamos el porcentaje como un factor de conversión.
Sabemos que hay 2.00 g de soluto en cada 100 g de solución.
Podemos invertir esto: Se necesitan 100 g de solución para tener 2.00 g de soluto.
Cálculo de la Solución Total
Usamos nuestro soluto real (10.0 g) para averiguar cuánta solución total necesitamos:
| 10.0 |
x | 100 g Solución | = | 500 g Solución Total |
| 2.00 |
El Paso Final (Deducción)
¡Cuidado! 500 g es el peso de toda la mezcla. Pero nos piden el agua.
Agua = Solución Total - Soluto
Agua = 500 g - 10.0 g = 490 g de Agua
Caso Especial: Cuando tenemos Volumen pero necesitamos Masa
En el laboratorio, a menudo es más fácil medir el volumen de un líquido que pesarlo. Sin embargo, para calcular el % m/m necesitamos obligatoriamente la masa. Aquí es donde la densidad (ρ = m/V) se convierte en nuestra herramienta clave para convertir de volumen a masa.
Ejemplo N° 4 (Densidad)
Se tienen 250 mL de una solución de ácido sulfúrico cuya densidad es de 1.05 g/mL. Si esta solución contiene 30.0 g de soluto puro, ¿cuál es su % m/m?
1. Análisis de Datos:
- Masa de soluto = 30.0 g
- Volumen de solución = 250 mL
- Densidad de solución = 1.05 g/mL
2. Conversión de Volumen a Masa (Método del Factor Unitario):
Utilizamos la densidad como un factor de conversión para transformar los mL de solución a gramos.
| 250 |
x | 1.05 g Solución | = | 262.5 g Solución |
| 1 |
3. Cálculo del % m/m:
| 30.0 g Soluto | x 100 = | 11.43 % m/m |
| 262.5 g Solución |
Ejemplo N° 5 (Conversión Instantánea)
Usando el método de Cadena de Factores, podemos convertir una concentración a otra en una sola línea, sin fórmulas intermedias.
Problema: Convertir una solución de KCl al 15.0% m/v (Densidad = 1.10 g/mL) a % m/m.
1. Estrategia Directa (Cadena de Factores):
Partimos de la definición: 15.0 g Soluto en 100 mL Solución. Queremos llegar a % m/m (g Soluto / g Solución).
2. Cálculo en una sola línea:
| 15.0 g Soluto | x | 1 mL Solución | x 100 = | 13.63 % m/m |
| 100 mL Solución | 1.10 g Solución |
Nota: Usamos la densidad invertida (1 mL / 1.10 g) para cancelar los mL de solución.
Ejemplo N° 6 (Reversa con Densidad)
Problema: Se requieren 15.0 g de KOH para un experimento. En el estante hay una solución al 25.0% m/m con densidad de 1.20 g/mL. ¿Qué volumen de esta solución debemos servir?
1. Estrategia (Cadena de Factores):
Necesitamos convertir: g Soluto → g Solución → mL Solución.
2. Cálculo:
| 15.0 g Soluto | x | 100 g Solución | x | 1 mL Solución | = | 50.0 mL Solución |
| 25.0 g Soluto | 1.20 g Solución |
Nota: Primero usamos el % invertido para hallar gramos de solución, luego la densidad invertida para hallar volumen.
2. Porcentaje en Volumen (% v/v): El Misterio
¡Advertencia Contraintuitiva!
En química, 50 mL + 50 mL ≠ 100 mL
A diferencia de la masa (que siempre se conserva), el volumen puede "encogerse" al mezclar líquidos.
La Analogía: Pelotas de Tenis y Arena
Imagina un balde lleno de pelotas de tenis (Moléculas grandes, como Etanol) y otro balde lleno de arena (Moléculas pequeñas, como Agua).
Si viertes la arena sobre las pelotas, la arena llenará los huecos vacíos. El volumen final será menor a la suma de los dos baldes originales.
Esto ocurre por los Puentes de Hidrógeno. Las moléculas de agua se "acomodan" fuertemente entre las moléculas de alcohol, contrayendo el volumen total de la mezcla.
La Fórmula
| % v/v = | Volumen de Soluto (mL) | x 100 |
| Volumen de Solución (mL) |
Ejemplo N° 7 (Contextualizado)
"Calcule el % v/v de una solución preparada mezclando 25.0 mL de alcohol con suficiente agua para dar un volumen total de 125 mL."
Nota de Experto: Fíjate que dice "suficiente agua para...". No dice "agregar 100 mL de agua". Esto es porque debido a la contracción, probablemente necesitemos un poco más de 100 mL de agua para llegar a la marca exacta de 125 mL.
Cálculo con Factor Unitario:| 25.0 mL Soluto | x 100 = | 20.0 % v/v |
| 125 mL Solución |
Ejemplo N° 8 (Cálculo de Volumen de Soluto)
Problema: ¿Cuánto alcohol puro (soluto) hay en una botella de vino de 750 mL al 12.0% v/v?
1. Estrategia:
Usamos el % como factor: 12.0 mL Soluto / 100 mL Solución.
2. Cálculo:
| 750 mL Solución | x | 12.0 mL Soluto | = | 90.0 mL Alcohol |
| 1 | 100 mL Solución |
Ejemplo N° 9 (Cálculo de Volumen de Solución)
Problema: Tenemos 50.0 mL de ácido acético. ¿Qué volumen de vinagre (solución al 5.00% v/v) podemos preparar con esto?
1. Estrategia:
Invertimos el factor %: 100 mL Solución / 5.00 mL Soluto.
2. Cálculo:
| 50.0 mL Soluto | x | 100 mL Solución | = | 1000 mL de Vinagre |
| 1 | 5.00 mL Soluto |
3. Porcentaje Masa-Volumen (% m/v): El Híbrido
Muy común en medicina (sueros salinos) porque es fácil de preparar: pesas la sal (precisión) y llenas con agua (velocidad).
La Fórmula
| % m/v = | Masa de Soluto (g) | x 100 |
| Volumen de Solución (mL) |
Ejemplo N° 10
Calcule el % (m/v) si disolvemos 22.0 g de metanol para dar 100 mL de solución.
| 22.0 g Soluto | x 100 = | 22.0 % m/v |
| 100 mL Solución |
Profundizando: ¿Por qué los volúmenes no se suman?
La realidad de las soluciones: Vsoluto + Vsolvente ≠ Vsolución
A diferencia de la masa, el volumen no es una propiedad conservativa en las mezclas. En termodinámica, esto se explica mediante el concepto de Volumen Molar Parcial: el volumen que ocupa una molécula depende de su entorno y sus vecinas.
-
1. Idealidad vs. Realidad:
Solo en una solución ideal (donde las moléculas son casi idénticas en tamaño y fuerzas, como benceno y tolueno) los volúmenes son aditivos. En la mayoría de soluciones reales, esto no ocurre. -
2. Interacciones (Ej. Contracción):
Si las moléculas de soluto y solvente se atraen con más fuerza que a sí mismas (como el etanol y el agua formando puentes de hidrógeno), la estructura se "aprieta" y el volumen total disminuye notablemente. -
3. Geometría y Empaquetamiento:
Independientemente de las fuerzas, las diferencias de tamaño y forma permiten que moléculas pequeñas ocupen el "volumen libre" o huecos entre las grandes, similar a cómo la arena puede llenar los espacios entre piedras.
La Regla de Oro
Debido a esta incertidumbre, en química analítica ignoramos el volumen del solvente y nos enfocamos únicamente en el volumen final de la solución, el cual medimos con precisión usando un matraz aforado.

Esta serie de 24 ejercicios te guiará desde lo básico hasta el dominio total del cálculo de soluciones.
I. Porcentaje Masa/Masa (% m/m)
1. Cálculo Directo
Se disuelven 15.0 g de NaCI en 85.0 g de agua. Calcule el % m/m de la solución.
1. Datos: Soluto = 15.0 g | Solvente = 85.0 g
2. Solución Total: 15.0 g + 85.0 g = 100.0 g
3. Cálculo (Factor Unitario):
| 15.0 g Soluto | x 100 = | 15.0 % m/m |
| 100.0 g Solución |
2. Interpretar Solución Total
Se tienen 5.0 g de azúcar disueltos en una solución cuya masa total es de 25.0 g. Calcule el % m/m.
1. Datos: Soluto = 5.0 g | Solución = 25.0 g (¡Ojo! Ya es el total)
2. Cálculo:
| 5.0 g Soluto | x 100 = | 20.0 % m/m |
| 25.0 g Solución |
3. Encontrar Soluto (Inverso)
¿Cuántos gramos de KCl se necesitan para preparar 500 g de una solución al 5.0 % m/m?
1. Estrategia: Usar el % como factor. 5.0% significa: "5.0 g Soluto por cada 100 g Solución".
2. Cálculo:
| 500 g Solución | x | 5.0 g Soluto | = | 25.0 g KCl |
| 100 g Solución |
4. Encontrar Solvente (Agua)
Si disuelves 10.0 g de sal para hacer una solución al 4.0 % m/m, ¿cuánta agua usaste?
1. Paso A (Solución Total): Sabemos que 4.0 g Soluto <-> 100 g Solución.
| 10.0 g Soluto | x | 100 g Solución | = | 250 g Solución Total |
| 4.0 g Soluto |
2. Paso B (Restar): Agua = Solución - Soluto
250 g - 10.0 g = 240 g de Agua
5. Contexto Real (Cocina)
Un chef tiene 1000 g de agua y quiere hacer una salmuera al 10.0% m/m. ¿Cuánta sal debe agregar? (¡Cuidado! El agua es el solvente, no la solución).
1. Análisis: Si la solución es 10% Sal, entonces el 90% es Agua (100 - 10).
2. Estrategia: Usar la relación Sal/Agua directamente -> 10 g Sal / 90 g Agua.
3. Cálculo:
| 1000 g Agua | x | 10 g Sal | = | 111.1 g Sal |
| 90 g Agua |
Nota: Si usaras 1000 g como solución, te daría 100g de sal, ¡y estaría incorrecto!
II. Porcentaje Volumen/Volumen (% v/v)
6. Dilución Correcta
Se toman 50 mL de etanol y se agrega agua hasta alcanzar un volumen final de 200 mL. Calcule el % v/v.
1. Datos: Soluto = 50 mL | Solución = 200 mL (Ya incluye la contracción).
2. Cálculo:
| 50 mL Soluto | x 100 = | 25.0 % v/v |
| 200 mL Solución |
7. Etiqueta de Farmacia
Una botella de alcohol medicinal de 500 mL dice "70% v/v". ¿Cuánto alcohol puro contiene?
1. Estrategia: 70% v/v significa 70 mL Alcohol por cada 100 mL Solución.
2. Cálculo:
| 500 mL Solución | x | 70 mL Alcohol | = | 350 mL Alcohol puro |
| 100 mL Solución |
8. Dilución de Laboratorio
Un técnico pipetea 10 mL de ácido acético y los vierte en un matraz aforado de 100 mL, llenando luego con agua hasta la marca. ¿Cuál es el % v/v?
1. Datos: Soluto = 10 mL | Solución Final = 100 mL.
2. Cálculo:
| 10 mL | x 100 = | 10.0 % v/v |
| 100 mL |
9. Preparación "Suficiente Agua"
Deseas preparar 250 mL de solución de acetona al 10.0% v/v. ¿Cuál es el procedimiento correcto?
1. Calcular Soluto Requerido:
| 250 mL Solución | x | 10 mL Acetona | = | 25 mL Acetona |
| 100 mL Solución |
2. Procedimiento: Medir 25 mL de acetona y agregar agua hasta completar 250 mL de volumen total (No agregar 225 mL de agua ciegamente por la contracción de volumen).
10. Volumen de Solución Total (% v/v)
Se requiere preparar una solución al 12.0% v/v de acetona. Si dispones de 50.0 mL de acetona pura, ¿cuántos mililitros de solución puedes preparar?
1. Estrategia: Invertir el factor %. 12.0 mL Soluto → 100 mL Solución.
2. Cálculo:
| 50.0 mL Soluto | x | 100 mL Solución | = | 416.7 mL Solución |
| 12.0 mL Soluto |
11. Interpretación de Vino
Una botella de vino de 750 mL tiene una concentración de 13.5% v/v. ¿Cuántos mL de alcohol ingieres si bebes media botella?
1. Volumen Consumido:
| 750 mL | = | 375 mL de vino |
| 2 |
2. Cálculo de Alcohol:
| 375 mL Vino | x | 13.5 mL Alcohol | = | 50.6 mL Alcohol |
| 100 mL Solución |
III. Porcentaje Masa/Volumen (% m/v)
12. Suero Fisiológico
Para preparar 1.0 Litro (1000 mL) de suero fisiológico al 0.9% m/v, ¿cuánta sal (NaCl) necesitas?
1. Estrategia: 0.9% m/v = 0.9 g Soluto / 100 mL Solución.
2. Cálculo:
| 1000 mL Solución | x | 0.9 g NaCl | = | 9.0 g NaCl |
| 100 mL Solución |
13. Bolsa de Dextrosa
Una bolsa de IV contiene 250 mL de Dextrosa al 5.0% m/v. ¿Cuántos gramos de azúcar recibe el paciente?
1. Cálculo:
| 250 mL Solución | x | 5.0 g Dextrosa | = | 12.5 g Dextrosa |
| 100 mL Solución |
14. Preparación de Reactivo
Disuelves 2.0 g de un colorante y llenas con agua hasta 50 mL. Calcule el % m/v.
1. Cálculo:
| 2.0 g Soluto | x 100 = | 4.0 % m/v |
| 50 mL Solución |
15. Encontrar Volumen
Necesitas exactamente 10.0 g de NaOH para una reacción. Tienes una solución stock al 20.0% m/v. ¿Qué volumen mides?
1. Estrategia: Invertir el factor. 20 g / 100 mL -> 100 mL / 20 g.
2. Cálculo:
| 10.0 g NaOH | x | 100 mL Solución | = | 50.0 mL |
| 20.0 g NaOH |
16. Procedimiento Correcto
Describe cómo preparar 500 mL de solución de AgNO3 al 2.0% m/v.
1. Cálculo de Soluto:
| 500 mL Solución | x | 2.0 g AgNO3 | = | 10.0 g AgNO3 |
| 100 mL Solución |
2. Paso a Paso:
- Pesar 10.0 g de AgNO3 en una balanza.
- Colocarlos en un matraz aforado de 500 mL.
- Agregar un poco de agua destilada y agitar para disolver.
- Agregar más agua hasta la marca de aforo (menisco).
IV. Desafíos Maestros (Nivel Experto)
17. Lectura de Etiquetas
Una lata de cerveza de 355 mL indica "5.0% Vol". ¿Cuántos mL de etanol puro contiene? ¿Y si tomas un "six-pack" (6 latas)?
1. Una Lata:
| 355 mL Cerveza | x | 5.0 mL Alcohol | = | 17.75 mL Alcohol |
| 100 mL Cerveza |
2. Six-Pack:
| 17.75 mL | x | 6 | = | 106.5 mL Alcohol (¡Más de media taza!) |
18. Doble Porcentaje
Mezclas 40 g de azúcar con 60 g de agua. El volumen final de la solución es de 80 mL (ojo: contracción/densidad). Calcule % m/m y % m/v.
1. Datos: Soluto = 40 g | Solvente = 60 g | Solución(masa) = 100 g | Solución(vol) = 80 mL.
2. % Masa/Masa:
| 40 g Soluto | x 100 = | 40.0 % m/m |
| 100 g Solución |
3. % Masa/Volumen:
| 40 g Soluto | x 100 = | 50.0 % m/v |
| 80 mL Solución |
Nota cómo el mismo jarabe tiene dos % diferentes dependiendo de la unidad.
19. Conversión con Densidad
Una solución al 20% m/m tiene una densidad de 1.15 g/mL. ¿Cuál es su % m/v?
1. Base de Cálculo: Imagina 100 g de solución.
- Masa Soluto = 20 g
- Masa Solución = 100 g
2. Convertir masa solución a volumen: (Vol = Masa / Densidad)
| 100 g | = | 86.96 mL |
| 1.15 g/mL |
3. Calcular % m/v:
| 20 g Soluto | x 100 = | 23.0 % m/v |
| 86.96 mL Solución |
20. Error Común
Un estudiante agrega 10 g de sal a 100 mL de agua. ¿Es esto una solución al 10% m/v?
Respuesta: NO EXACTAMENTE.
Al agregar sal al agua, el volumen aumentará ligeramente (aunque poco). Si el volumen final es 102 mL, por ejemplo, el % sería:
| 10 g | = | 9.8% m/v |
| 102 mL |
Para hacerla exactamente al 10%, debió disolver la sal en menos agua y luego aforar (completar) a 100 mL.
21. El Riego por Goteo
Un sistema de riego necesita 500 Litros de solución de fertilizante al 0.05% m/v. ¿Cuántos gramos de fertilizante sólido necesitas comprar?
1. Convertir Litros a mL:
| 500 L | x | 1000 mL | = | 500,000 mL |
| 1 L |
2. Cálculo:
| 500,000 mL Solución | x | 0.05 g Fertilizante | = | 250 g Fertilizante |
| 100 mL Solución |
22. Cálculo con Densidad (Tipo Ejemplo 4)
Se tienen 200 mL de una solución de ácido nítrico cuya densidad es de 1.10 g/mL. Si esta solución contiene 22.0 g de soluto puro, ¿cuál es su % m/m?
1. Estrategia: Tenemos Volumen, pero el % m/m requiere Masa de Solución. Usamos la densidad para convertir.
2. Conversión (Volumen -> Masa):
| 200 mL Solución | x | 1.10 g Solución | = | 220 g Solución |
| 1 mL Solución |
3. Cálculo Directo (% m/m):
| 22.0 g Soluto | x 100 = | 10.0 % m/m |
| 220 g Solución |
23. De % m/m a % m/v (Puente de Densidad)
El ácido clorhídrico concentrado comercial se vende al 37.0% m/m y tiene una densidad de 1.19 g/mL. Calcule su concentración en % m/v.
1. Estrategia Directa (Cadena de Factores):
Para encontrar el % m/v, necesitamos saber cuántos gramos de soluto hay en 100 mL de solución. Por lo tanto, empezamos nuestro cálculo con 100 mL.
2. Cálculo en una sola línea:
| 100 mL Solución | x | 37.0 g Soluto | x | 1.19 g Solución | = | 44.03 g Soluto (en 100 mL) |
| 100 g Solución | 1 mL Solución |
Resultado: 44.03 % m/v
Nota: Aquí ordenamos los factores para usar los datos tal cual nos los dan (% y densidad), cancelando los mL al final y los g de solución al medio.
24. Extracción de Soluto Líquido
Necesitas obtener 50.0 g de soluto puro para una reacción. Dispones de una solución líquida concentrada al 40.0% m/m con densidad de 1.25 g/mL. ¿Qué volumen de esta solución debes medir en una probeta?
1. Estrategia (Cadena de Factores Unitarios):
g Soluto → g Solución → mL Solución
2. Cálculo Integrado:
| 50 g Soluto | x | 100 g Solución | x | 1 mL Solución | = | 100.0 mL Solución |
| 40 g Soluto | 1.25 g Solución |
¡Observa cómo se cancelan las unidades en cadena!