Instrucciones
Usted tiene las siguientes opciones en este simulador para moléculas pequeñas tanto inorgánicas como orgánicas.
- En la parte superior, aparecen los botones 2D y 3D para que pueda observar el modelo en dos o tres dimensiones.
- A continuación se presenta el modelo en dos o tres dimensiones.
- "Search" puede ser utilizado para buscar alguna molécula, escribiendo el nombre en inglés, por ejemplo al escribir, sulphuric acid (ácido sulfúrico).
- Color de fondo, sirve seleccionar el color del fondo del modelo en tres dimensiones.
- Acercar +, acerca el modelo.
- Acercar -, aleja el modelo.
- Girar X, Y, Z, para girar el modelo en tres dimensiones en los ejes x, y, z.
- Alambres, varillas y pelotas y varillas, para cambiar el modelo en tres dimensiones en esas representaciones.
- Energía, aparce en la parte superior la energía de la molécula en kJ/mol o kcal/mol.
- Minmizar por MMFF94, normalmente las estructuras iniciales que se crean en los simuladores poseen energías mucho mayores a las que tendría un objeto real, por esta razón, se utilizan algoritmos para calcular las posiciones y fuerzas originales, con el objetivo de minimizarlas y que sean más realistas.
- Arrastrar Minimizar, usted puede arrastrar un átomo, soltarlo y entonces el sistema hace un cálculo de minimización de energía.
- Simetría, muestra los planos de simetría en la molécula.
- Editar, puede editar la molécula agragando o quitando átomos y enlaces.
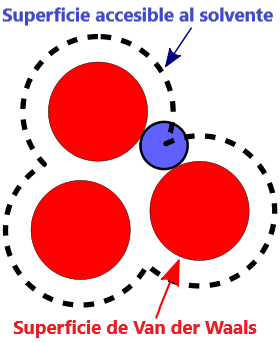
- Superficie VDW, la superficie de van der Waals de una molécula es una representación abstracta o modelo de esa molécula, que ilustra dónde, en términos muy generales, podría haber una superficie para la molécula en función de los cortes duros de los radios de van der Waals para átomos individuales, y representa una superficie a través de la cual la molécula podría concebirse interactuando con otras moléculas.
- PEM es el mapa de potencial electrostático.
- Carga parcial calcula la carga parcial de cada átomo.
- Tetraedros, para el caso que exista alguna átomo tetraédrico.
- Dipolos enlaces, para ver el los dipolos de todos los enlaces.
- Dipolo molecular, para ver el momento dipolar resultante de toda la molécula.
- Hibridación sp, sp2 y sp3, para ver la hibridacion del átomo de carbono.
- Anillo aromático, muestra los anillos aromáticos.
- Heteroátomo, muestra los heteroátomos en heterociclos.
- C quiral (nomenclatura R/S) y E/Z para isomería geométrica en alquenos, los descriptores R/S permiten indicar en un compuesto orgánico la configuración (la disposición espacial de los sustituyentes) de un carbono o centro quiral, estereocentro o centro estereogénico, que es el caso de un átomo de carbono con cuatro sustituyentes diferentes. Se añade R o S entre paréntesis como prefijo delante del nombre de la molécula orgánica. En caso de ser más de uno el centro estereogénico, separados por coma se indica el descriptor R o S de cada uno, precedido del número o localizador que identifica su posición.
- Invertir R/S, para cambiar la quiralidad.
- Nomenclatura E/Z en Alquenos, el sistema tradicional para nombrar los isómeros geométricos de un alqueno, en el que los mismos grupos están dispuestos de manera diferente, es nombrarlos como cis o trans. Sin embargo, es fácil encontrar ejemplos donde el sistema cis-trans no se aplica fácilmente.
- N electrones, O electrones y S electrones, para ver los electrones libres del nitrógeno, oxígeno y azufre.
- C primario, C secundario, C terciario, C cuaternario, identifica la clasificación de los átomos de carbono.
- Dadores y aceptores de puentes de hidrógeno, señala los átomos que pueden dar o aceptar puentes de hidrógeno
- Botón 2D, cuando escoge el botón 2D, la aplicación tiene su propio menú y quedan inhabilitados todos los botones 3D.
Laboratorio de IA: Tu Copiloto de Estudio
Aprende a usar la Inteligencia Artificial
La IA (como ChatGPT, Gemini o Copilot) no sirve solo para darte respuestas. Úsala para profundizar tu pensamiento crítico. Aquí tienes 3 "Prompts" avanzados para desafiar tu comprensión:
1. Desmitificando el Equivalente
Entiende el 'por qué' de la N.
2. Detective de Titulación
Lógica detrás de NaVa = NbVb.
3. Molaridad vs. Normalidad
Análisis crítico de unidades.
Soluciones

Podcast: Entendiendo la Normalidad
Escucha la explicación conceptual sobre Equivalentes y Normalidad.
Video Explicativo
Presentación Resumida
Para mejor experiencia en celular, abre la guía directamente:
Abrir Guía PDFVisualiza las diapositivas clave del tema.
Infografía Resumen

Guía visual rápida sobre conceptos clave.
El Problema: ¿Por qué la Molaridad no basta?
Imagina que tienes dos matraces en el laboratorio: uno con ácido clorhídrico (HCl) 1.0 M y otro con ácido sulfúrico (H2SO4) 1.0 M. Si quisieras neutralizarlos con una base fuerte, ¿necesitarías el mismo volumen para ambos?
La intuición, pensando solo en Molaridad, nos dice que sí. Sin embargo, la respuesta es NO.
El ácido sulfúrico tiene la capacidad de liberar dos protones (H+) por molécula, el doble que el clorhídrico. Aunque tengan la misma concentración de moléculas (Molaridad), el sulfúrico tiene el doble de capacidad reactiva. Aquí nace la necesidad de una métrica que mida esa capacidad real: la Normalidad.

Paso 1: La Pieza Clave (Peso Equivalente)
Para comparar "manzanas con manzanas", necesitamos medir la masa de sustancia que aporta una unidad de reacción. A esto le llamamos Peso Equivalente (Peq).
- El peso equivalente de un ácido es la masa (g) que produce 1 mol de H+.
- El peso equivalente de una base es la masa (g) que produce 1 mol de OH-.
Ejemplo N° 1
En la reacción del H2SO4 donde ambos iones H+ son reemplazados:
| 98 g/mol |
| 2 eq/mol |
Resumiendo, el peso equivalente se calcula así:
| Peso Molar (g/mol) |
| # de H+, OH- o Carga Total |
Ejemplo N° 2
Calcular el peso equivalente de:
- H2SO4 (se reemplaza 1 H+):
Peq =
= 98.0 g/eq98.0 g/mol 1 eq/mol - Ca(OH)2 (ambos OH- reemplazados):
Peq =
= 37.05 g/eq74.1 g/mol 2 eq/mol - HCl:
Peq =
= 36.5 g/eq36.5 g/mol 1 eq/mol - En Redox: es 1 mol de electrones (e-).
Ejemplo: MnO4- + 5e- → Mn+2
Aquí, 1 mol de Permanganato consume 5 moles de electrones, así que su Peq se divide entre 5. - En Ácido-Base/Sales (como este ejemplo): es 1 mol de protones (H+).
- Si tienes una sal simple como NaCl (Na+), cada molécula aporta una moneda de +1.
- Pero si tienes CaSO4 (Ca+2), cada molécula trae una moneda de valor +2. Para obtener un valor unitario de +1, necesitarías (conceptualmente) solo la mitad de la molécula.
- El corazón y las células nerviosas funcionan con corrientes eléctricas (Na+, K+, Cl-).
- Lo vital es la cantidad de carga disponible, no la masa del átomo.
- Ejemplo: 1 mEq de Sodio (Na+) tiene el mismo efecto eléctrico que 1 mEq de Potasio (K+), aunque tengan masas muy diferentes.
- Física: Así como "Joule" unifica calor y trabajo mecánico, el "Equivalente" unifica ácidos, bases y oxidantes en una sola unidad de "Poder Reactivo".
- Matemática: Simplifica modelos complejos. Al usar Equivalentes, eliminamos la necesidad de coeficientes estequiométricos (1:1 siempre), haciendo el Análisis Dimensional mucho más limpio.
- AlCl3 (Al+3):
En el caso del AlCl3, el Aluminio tiene carga +3. Si piensas en cómo se formó esta sal, el Aluminio tuvo que reemplazar a 3 hidrógenos del ácido original (3 HCl).
Como un solo átomo de Al+3 hizo el trabajo de 3 protones (H+), decimos que 1 mol de AlCl3 equivale a 3 equivalentes de ácido. Por tanto, para encontrar la masa de "una sola unidad de sustitución", dividimos su peso entre 3.Reacción de formación (Ácido-Base):
Al(OH)3 + 3 HCl → AlCl3 + 3 H2OPerspectiva Redox (Desde elementos):
2 Al0 + 3 Cl20 → 2 AlCl3
Aunque en total se transfieren 6 electrones (2 átomos × 3), el PEq es por mol.
6 electrones / 2 moles = 3 eq/mol.Peq =
= 44.43 g/eq133.3 g/mol 3 eq/mol - CaSO4 (Ca+2):
En el caso del CaSO4, el Calcio tiene carga +2. Si piensas en cómo se formó esta sal, el Calcio tuvo que reemplazar a 2 hidrógenos del ácido original (H2SO4).
Como un solo átomo de Ca+2 hizo el trabajo de 2 protones (H+), decimos que 1 mol de entre 2.Reacción de formación (Ácido-Base):
Ca(OH)2 + H2SO4 → CaSO4 + 2 H2OPerspectiva Redox (Metal + Ácido):
Ca0 + H2SO4 → CaSO4 + H2
Aquí el Calcio transfirió 2 electrones (de 0 a +2).
(2 electrones = 2 equivalentes).Peq =
= 68.05 g/eq136.1 g/mol 2 eq/mol - Al2(SO4)3 (2 × Al+3 = 6):
En el caso del Al2(SO4)3, tenemos 2 átomos de Aluminio (+3 c/u), dando una carga total de +6. Si piensas en la formación, estos 2 aluminios reemplazaron a 6 hidrógenos (provocados por 3 moléculas de H2SO4).
Como la unidad fórmula completa hizo el trabajo de 6 protones, decimos que 1 mol de sal equivale a 6 equivalentes. Por tanto, dividimos su peso entre 6.Reacción de formación (Ácido-Base):
2 Al(OH)3 + 3 H2SO4 → Al2(SO4)3 + 6 H2OPerspectiva Redox (Metal + Ácido):
2 Al0 + 3 H2SO4 → Al2(SO4)3 + 3 H2
Aquí los 2 Aluminios transfirieron 6 electrones en total.
(2 átomos × 3 electrones = 6 equivalentes).Peq =
= 57.02 g/eq342.1 g/mol 6 eq/mol
Ejemplo N° 3 (Sales)
Para las sales, el concepto es similar pero nos enfocamos en la carga. El Peso Equivalente es el peso fórmula dividido por la carga total positiva del metal (catión).
¿Por qué dividimos por la carga total?
La Explicación Teórica:
La definición más general dice que un equivalente es la cantidad que transfiere una unidad
de
carga.
Aunque la reacción
Al(OH)3 + 3 HCl no es Redox (no hay
transferencia de electrones en este momento), el número es el mismo.
El Aluminio tiene carga +3 porque le "faltan" 3 electrones. Esto lo hace químicamente
equivalente a 3 protones (H+), ya que a cada protón también le "falta" 1
electrón.
Ambos conceptos miden lo mismo: Capacidad de Carga.
A continuación detallamos el razonamiento para cada caso específico:
La Analogía (Para recordarlo mejor):
Piénsalo así: Un "Equivalente" es como una moneda de cambio universal con valor de
+1.
Por eso, para "estandarizar" todo a unidades de carga +1, dividimos la masa total entre la única "moneda" que importa: la carga.
Ciencias de la Salud
En Medicina, no usamos "gramos" para los electrolitos en sangre, usamos Miliequivalentes (mEq).
Física y Matemática
Este concepto es pura Estandarización y belleza matemática:
Visualización en una Reacción
Observa cómo los equivalentes se conservan en la formación de la sal:
2 Al(OH)3 + 3 H2SO4 → Al2(SO4)3 + 6 H2O
| Base | Ácido | Sal Formada |
|---|---|---|
| 2 moles × (3 OH-) | 3 moles × (2 H+) | 1 mol × (Qtot = +6) |
| = 6 Equivalentes | = 6 Equivalentes | = 6 Equivalentes |
Error Común: Carga en Sales
En el caso del Al2(SO4)3, un error frecuente es usar solo la carga de un ion (+3). Recuerda que debes usar la carga total: 2 iones de Aluminio × (+3) = +6 total de carga positiva.
Paso 2: Conversión Clínica: mg vs mEq
En el ámbito clínico, es crucial convertir entre la masa de medicamento (mg) y su actividad electrónica (mEq).
Fórmulas de Conversión
De masa a equivalentes:
| mEq = | mg × Valencia |
| Peso Atómico |
De equivalentes a masa:
| mg = | mEq × Peso Atómico |
| Valencia |
Método del Factor Unitario (Recomendado)
En lugar de memorizar fórmulas, usa el Peso Equivalente (Peq) como puente de conversión.
De mg → mEq:
| 1 mEq |
| Peq (mg) |
De mEq → mg:
| Peq (mg) |
| 1 mEq |
* Recuerda que Peq = Peso Molecular / Valencia
Caso 1: mg → mEq
| Ion | Masa (mg) | Cálculo | Resultado | ||
|---|---|---|---|---|---|
| Na+ (23 g/mol) | 230 mg |
|
10 mEq | ||
| Ca++ (40 g/mol) | 200 mg |
|
10 mEq | ||
| K+ (39 g/mol) | 78 mg |
|
2 mEq |
Caso 2: mEq → mg
| Ion | mEq | Cálculo | Resultado (mg) | ||
|---|---|---|---|---|---|
| Na+ (Salina) | 154 mEq |
|
3542 mg | ||
| Mg++ (24 g/mol) | 20 mEq |
|
240 mg | ||
| Cl- (35.5 g/mol) | 100 mEq |
|
3550 mg |

Desafíos Clínicos: ¿Te atreves a resolverlos?
Usa la etiqueta del suero de arriba y las fórmulas para resolver estos casos reales. (Haz clic para ver la respuesta).
1. Interpretando la Etiqueta (K+)
2. Interpretando la Etiqueta (Na+)
3. Preparando una solución (Gluconato de Ca)
4. Corrigiendo Potasio (KCl)
5. Sintetizando la información (Cálculo Inverso)
5. Verificando el Potasio (K+)
6. Verificando el Sodio (Na+)
7. Orden Médica: Calcio
8. Orden Médica: Potasio
Paso 3: La Normalidad
Con el concepto de peso equivalente dominado, ya podemos generar nuestra unidad de concentración. La Normalidad (N) es simplemente el número de equivalentes por litro.
| # Equivalentes de Soluto |
| Litros de Solución |
O de forma simplificada:
N = M × Valencia
¿De dónde sale esta fórmula?
Es un simple análisis dimensional. Si multiplicamos la Molaridad por la Valencia, las unidades de "mol" se cancelan:
| moles |
| Litro |
| equivalentes |
| mol |
| equivalentes |
| Litro |
Por eso, si ya tienes la Molaridad, ¡no trabajes doble! Solo multiplícala por la valencia.
¿Por qué es tan importante la Normalidad?
La Normalidad no es solo "otra unidad más". Es la unidad que nos permite igualar capacidades de reacción. Mientras la Molaridad cuenta partículas, la Normalidad cuenta "poder de acción".
En Ciencias Médicas
- Equilibrio Electrolítico: Nuestro cuerpo no funciona por gramos de sodio o potasio, sino por sus cargas eléctricas. El corazón late gracias a diferencias de potencial generadas por estas cargas. Por eso los exámenes de sangre reportan en mEq/L (miliNormalidad).
- Fisiología Ácido-Base: Para regular el pH de la sangre (7.35-7.45), el cuerpo balancea equivalentes de ácidos y bases (como el Bicarbonato).
En Física y Matemática
- Estandarización y Vectores: Podríamos ver la Normalidad como una "magnitud vectorial" química. No solo importa la cantidad (magnitud molar), sino su "dirección" o capacidad de aporte (valencia).
- Simplificación Dimensional: Al usar Normalidad, la ecuación de neutralización se vuelve una igualdad lineal simple (V1·N1 = V2·N2), eliminando la necesidad de constantes de proporcionalidad complejas (coeficientes estequiométricos) en el cálculo. Es el "sistema de coordenadas" perfecto para reacciones.
Ejemplo N° 4
Normalidad de una solución de H3PO4 (2.50 g en 135 mL) donde se reemplazan los 3 hidrógenos:
Respuesta:
Solución (Método del Factor Unitario)
En lugar de hacerlo por pasos separados, podemos construir una sola "cadena" de conversión que nos lleve de los datos (gramos/mL) a la respuesta (eq/L).
|
× |
|
× |
|
× |
|
= | 0.567 N |
Análisis: Los "mL", "g" y "mol" se cancelan, dejándonos únicamente con eq arriba y L abajo.
Piénsalo un momento...
En el ejemplo anterior, la Normalidad es 0.567 N porque el ácido donó sus 3 protones. Pero en muchas reacciones bioquímicas (buffers), el H3PO4 solo dona 2 protones.
Reto: ¿Cómo cambiaría la Normalidad en ese caso? (Pista: Tu "n" ya no sería 3, sería 2. Esto demuestra que la Normalidad depende de la reacción específica, no solo de la sustancia).
Ejemplo N° 5
Gramos de H2SO4 necesarios para preparar 225 mL de solución 0.150 N (reemplazando ambos H):
Respuesta:
| 0.150 N × 98 g/mol × 0.225 L |
| 2 |
Paso 4: La Eficiencia (El secreto del laboratorio)
La razón histórica y práctica por la que usamos Normalidad es la eficiencia. Nos permite usar una fórmula universal para neutralizaciones y diluciones sin detenernos a calcular la estequiometría de cada reacción:
Esta "fórmula mágica" funciona siempre que usemos Normalidad.
Ejemplo N° 6
¿Qué volumen (en mL) de solución de NaOH 0.25 N contiene 1.5 gramos de soluto?
Respuesta:
| 1.5 g NaOH | × |
|
× |
|
× |
|
= | 150 mL |
Ejemplo N° 7 (Neutralización)
¿Cuántos mL de NaOH 0.1 N se necesitan para neutralizar 1.5 mL de HCl 0.15 N?
Datos:
- Ácido (HCl): Va = 1.5 mL, Na = 0.15 N
- Base (NaOH): Nb = 0.1 N
- Incógnita (Vb): ?
Principio de Neutralización:
(Eqácido = Eqbase)
Despejando el volumen de base (Vb):
Vb = (Va × Na) / NbSustitución:
| 1.5 mL × 0.15 N |
| 0.1 N |
Ejemplo N° 8 (Dilución)
Calcular cuántos mL de HCl 5.0 N se requieren para preparar 50.0 mL de ácido diluido 0.1 N.
Datos:
- Concentración Concentrada (N1): 5.0 N
- Volumen Diluido (V2): 50.0 mL
- Concentración Diluida (N2): 0.1 N
- Incógnita (V1): ?
Usamos la ecuación de dilución:
Despejando V1:
V1 = (V2 × N2) / N1Sustitución:
| 50.0 mL × 0.1 N |
| 5.0 N |